Robert T. Wainwright’s Partridge Puzzle for n=8 is: pack one 1x1 unit square, two 2x2 unit squares, … , eight 8x8 unit squares into a larger 36 x 36 square. Since the sum of the first n cubes is equal to the square of the sum of the first n integers, it shouldn’t be impossible for any n, but n=8 is the smallest value where a packing actually exists:

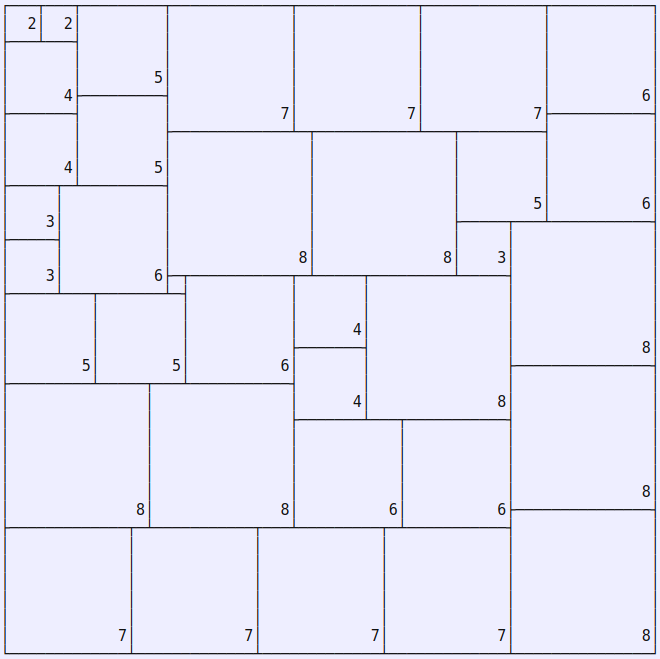
Partridge puzzle solution for n=8

(The little unlabled square above is 1x1, but it’s too tiny for a label.)

You can generate all solutions for n=8 at a terminal by running

examples/partridge/solve-partridge.sh 8

from github.com/aaw/cover and waiting a few minutes for the first one to appear.